Situation und Problem
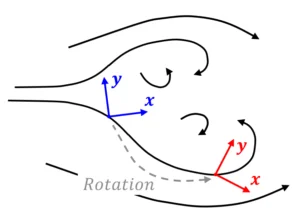
Turbulente Strömungen von Flüssigkeiten und Gasen («Fluiden») lassen sich schlecht modellieren, denn die einzelnen Fluidvolumen bewegen sich auf chaotischen Bahnen. Wenn die Anfangsbedingungen nur leicht geändert werden, kann es sein, dass ein einzelnes Fluidvolumen an einen komplett anderen Ort fliesst. Als einfaches Beispiel dieses Verhaltens kann ein Lorenz-Attraktor betrachtet werden (Abbildung 1):
Ein Startvolumen fliesst aufgrund minimaler Differenz des Startorts auf komplett unterschiedlichen Bahnen. Nach einer gewissen Zeit kann sich das Teilchen an gegenüberliegenden Orten auf der Gesamtkurve befinden.
Heutige Rechenmethoden berechnen deshalb dasselbe Problem viele Male hintereinander, jeweils mit leicht unterschiedlichen Anfangsbedingungen. So werden viele mögliche Bahnen ermittelt, welche dann wiederum ein stabiles Gesamtbild ergeben. Ein Beispiel für dieses «Ensemble-Prognose» genannte Vorgehen bildet die Vorhersage der Bahn des Hurrikans Fiona im September 2022 in Abbildung 2:
Natürlich steigt durch die Vielfachberechnung der Rechenaufwand enorm. Zudem ist nicht immer sicher, ob wirklich die wichtigen Bahnen berechnet wurden. Das Problem entsteht dabei dadurch, dass die einzelnen Bahnen ihre Aussagekraft verlieren, da sie sich durch eine leichte Änderung komplett anders verhalten.
Lösung
Bei erneuter Betrachtung des Lorenz-Attraktors aus Abbildung 1 fällt Folgendes auf: Obwohl das Verhalten des einzelnen Fluidvolumens praktisch nicht mehr vorhergesagt werden kann, entsteht übers Ganze gesehen eine geordnete Form.
Es ist demnach so, dass in vielen Fällen zwar die Bahn des einzelnen Fluidvolumens ihre Bedeutung verliert und keine nützliche Information mehr enthält, jedoch über alle Fluidvolumen summiert eine geordnete und oft sogar stationäre Form entsteht.
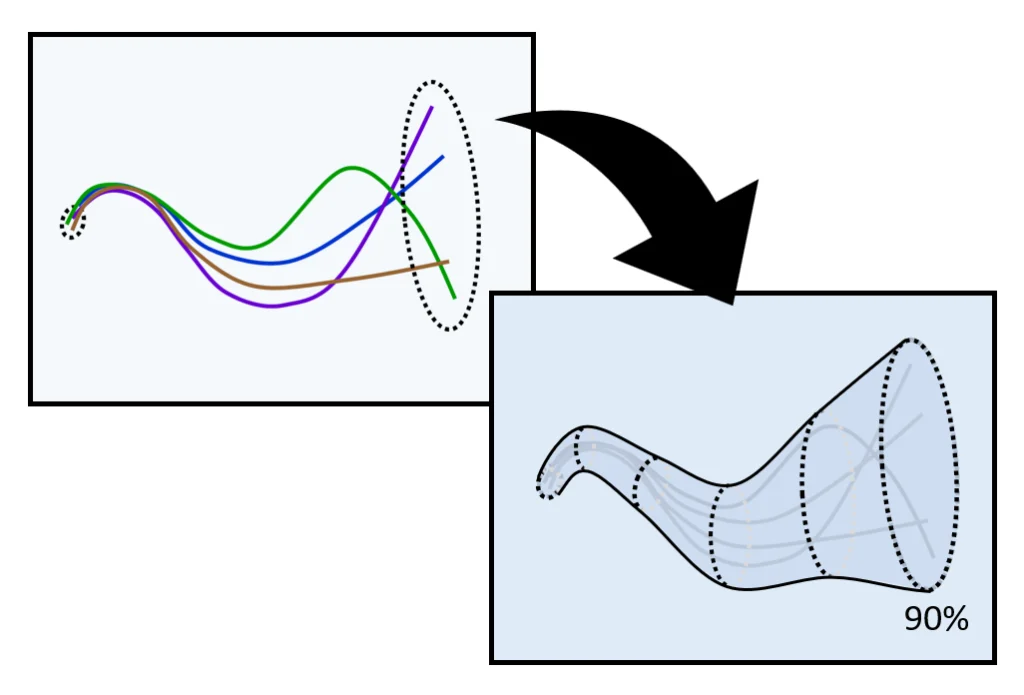
Eine Methode, welche über alle in der Startkonfiguration vorhandenen Fluidvolumen summieren und alle möglichen Bahnen gemeinsam betrachten kann, würde folglich direkt dieses Gesamtbild hervorbringen, ohne dass man sich um die einzelnen Bahnen kümmern muss (Abbildung 3).
Derartige Methoden wurden bereits für ein anderes Gebiet der Physik entwickelt, wo dasselbe Problem noch in verschärfter Form auftritt:
In der Quantenmechanik ist es unmöglich, die Bahn eines einzelnen Teilchens zu verfolgen. Deshalb wurden mächtige mathematische Werkzeuge entwickelt, welche es erlauben, eine statistische Analyse über alle möglichen Bahnen zu berechnen, selbst wenn die tatsächlich realisierten Bahnen unbekannt sind.
Die Idee der Quantenwirbeltheorie ist es, diese mathematischen Werkzeuge (genannt Quantenfeldtheorien QFT) für turbulente Strömungen zu verwenden. Die dadurch ermöglichte parallele Berechnung von vielen Bahnen steigert nicht nur die Effizienz der Kalkulation – sie erlaubt auch eine direkte Analyse der Gesamtströmung wenn es unmöglich wird, einzelne Fluidvolumen zu verfolgen.
Weiterführende Links
Die detaillierte mathematische Herleitung der Quantenwirbeltheorie ist in zwei wissenschaftlichen Manuskripten formuliert, welche als pdfs zum Download bereit stehen.