Situation und Problem
Das Verhalten eines viskosen Fluides lässt sich einfach anhand der Strömung zwischen zwei Platten veranschaulichen, wobei die untere Platte ruht, währendem die obere Platte nach rechts gezogen wird (Abbildung 1). Man stellt sich das Fluid dazwischen bestehend aus einzelnen Schichten vor:
Abbildung 1
Strömung zwischen einer ruhenden Platte (ganz unten, grau) und einer Platte, die nach rechts gezogen wird (oben). Dazwischen befinden sich Schichten des Fluides (blau).
Durch Reibung werden die einzelnen Schichten von der jeweils oberen Schicht mitgerissen und gleichzeitig von der unteren Schicht abgebremst. Je stärker diese Reibung zwischen den Schichten ist, desto höher ist die Viskosität eines Fluids.
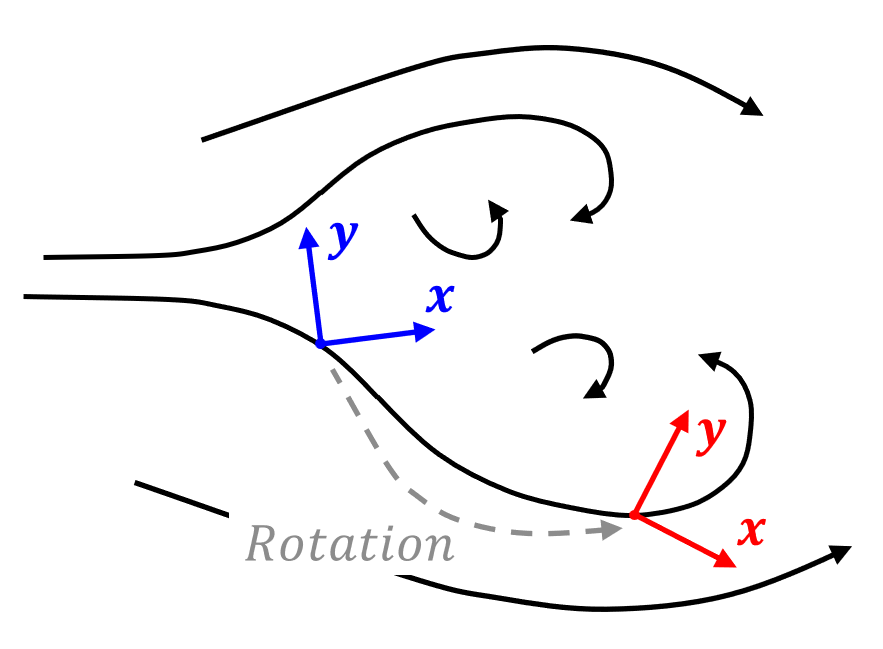
In realen Situationen fliessen die Fluidvolumen jedoch nicht nur in Schichten, sondern bewegen sich in alle Richtungen relativ zueinander. Dadurch ist es nötig, die Geschwindigkeitsunterschiede zwischen allen möglichen Bewegungsrichtungen zweier benachbarter Fluidvolumen zu berücksichtigen. Jedes Volumen kann sich dabei in alle drei Raumrichtungen bewegen (rote Pfeile in Abbildung 2). Unabhängig davon bewegt sich der Nachbar ebenfalls in drei Richtungen (blaue Pfeile):
Abbildung 2
Zwei benachbarte Fluidvolumen und mögliche Bewegungsrichtungen (rote und blaue Pfeile). Beide Volumen können sich jeweils auf drei Achsen bewegen: links-rechts, oben-unten oder vorne-hinten, hier genannt x, y und z.
Die demnach zu berücksichtigenden neun (3 × 3) unterschiedlichen Kombinationen werden als Matrix zusammengefasst, welche den Geschwindigkeitsgradienten bilden. Vereinfacht wird das Problem dadurch, dass für die Reibungskräfte nur die symmetrischen Anteile dieses Gradienten entscheidend sind, welche als Deformationsraten-Tensor 
ausgedrückt werden:
Wenn man mit dieser Matrix von Werten zu rechnen beginnt, wird es jedoch schnell sehr kompliziert. Die einzelnen Werte sind nicht eigenständig, sondern vermischen sich alle miteinander.
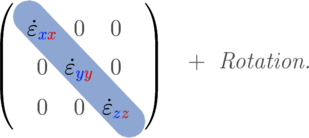
Interessant ist aber, dass es durch die Symmetrie des Deformationsraten-Tensors immer möglich ist, die Koordinaten x, y und z so zu rotieren, dass der Tensor Diagonalgestalt annimmt und alle Einträge ausserhalb der Matrix-Diagonalen verschwinden:
Dadurch werden nicht nur die Anzahl der Einträge reduziert, es ist auch so, dass sich die Diagonal-Einträge nicht mehr vermischen. Dieses besonders einfache Ideal-Koordinatensystem nennt man das Eigensystem des Problems.
Leider reicht dies zur Beschreibung von turbulenten Strömungen noch nicht. Es gibt zwar immer dieses ideale Eigensystem. Die Rotation, um in dieses zu gelangen, ist aber überall eine andere:
Abbildung 3
In einer turbulenten Strömung (angedeutet durch die schwarzen Pfeile) kann das Eigensystem an jedem Ort unterschiedlich angeordnet sein (rote und blaue Pfeile). Um überall in das Eigensystem gelangen zu können, muss an jedem Ort eine individuell angepasste Rotation erfolgen.
Lösung
Man muss also an jedem Ort eine eigene, massgeschneiderte Rotation durchführen können, welche das Koordinatensystem in das Eigensystem dreht. Es braucht nicht nur eine einzelne Drehung, sondern ein ganzes «Feld» von individuellen Drehungen an allen Orten. Mathematisch ausgedrückt, wird die einzelne Rotation R zu einem ortsabhängigen Feld von Rotationen R(x, y, z).
Dies ist die Neuerung zur Beschreibung eines Fluides mittels der Quantenwirbeltheorie. Der Ansatz lässt sich wie folgt darstellen:
Tatsächlich ist es gar nicht abwegig, ein solches Feld von Rotationen mathematisch zu formulieren. Denn obwohl die entstehenden Ausdrücke kompliziert werden, hat das Feld günstige mathematische Eigenschaften, die zudem aus der Quantenmechanik sehr genau bekannt sind. Mathematisch gesagt, bilden die Rotationen eine sogenannte Lie-Gruppe, und ein solches Feld von Rotationen wird «Eichfeld» genannt. Theorien, die mit derartigen Feldern arbeiten, heissen Quantenfeldtheorien (QFT).
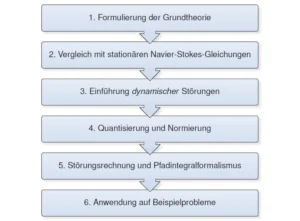
Der Ansatz bietet eine Aufteilung des Problems der turbulenten Strömungen in verschiedene Teilprobleme. Zunächst wird die lokale Formel maximal vereinfacht. Alles Komplizierte ist nicht verschwunden, sondern wird abgetrennt und befindet sich separiert im neuen Rotationsfeld. Dieses enthält gewissermassen die Information darüber, wie die lokalen Systeme im Verhältnis zueinander angeordnet sind und zusammenhängen.
Das Verhalten des entstandenen Feldes ist seinerseits aus der Standardliteratur bekannt, und es gibt leistungsstarke Methoden, welche es erlauben, die Information darin weiter aufzugliedern, die einzelnen Terme zu interpretieren und schlussendlich zu lösen.
Beim Anwenden dieser Rechenmethoden übertragen sich – praktisch als Bonus – die aus der Quantenmechanik bekannten Prinzipien der Summierung über alle möglichen Pfade und die Berechnung von Wahrscheinlichkeiten auf die Quantenwirbeltheorie (siehe dazu den vorhergehenden Text «1 – Grundidee»).
Eine versteckte Schwierigkeit bei diesem Vorgehen besteht darin, die Symmetrisierung des Deformationsraten-Tensors so durchzuführen, dass diese kompatibel ist mit dem Eichfeld-Ansatz. In der Herleitung wird dazu ein spannender Lösungsansatz verwendet, welcher dies mit einer adaptierten Polarzerlegung und einem einfachen Phasenfeld erreicht.
Weiterführende Links
Die detaillierte mathematische Herleitung der Quantenwirbeltheorie ist in zwei wissenschaftlichen Manuskripten formuliert, welche als pdfs zum Download bereit stehen.
