3 – Vorgehen

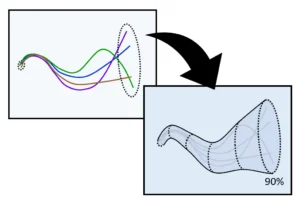
Im ersten Schritt wird die ortsabhängige Diago­nalisierung des Deformations­raten-Tensors durchgeführt. Da dieser Tensor symmetrisch ist, werden dafür Rotations­felder (SO(3)-Eichfelder) verwendet. Die Diago­nalisierung erfolgt zunächst global und anschließend lokal für inver­tier­bare, normale Matrizen. Die genaue Form der verwendeten SO(3)-Eichfelder wird dabei detailliert beschrieben.
Zur grundlegenden Theorie gehört auch die lokale Symme­trisierung des Deformations­raten-Tensors. Diese erfolgt durch eine lokale Polar­zerlegung, bei der ein zusätzliches U(1)-Phasenfeld verwendet wird, das senkrecht zu den SO(3)-Feldern steht.
Als dritter Punkt wird mithilfe des Material­gesetzes für viskose Fluide aus dem so erhaltenen Deformationsraten-‌Tensor der Cauchy-Spannungs­tensor hergeleitet.

Die Navier-Stokes-Gleichungen werden hergeleitet aus der Divergenz des Spannungs­tensors (siehe z.B. Herleitung der Impulsgleichung). Entsprechend wird die Divergenz des in Schritt 1 entwickelten Feld­ausdrucks für den Spannungs­tensor mit den Navier-Stokes-Gleichungen verglichen. Dieser Vergleich wird für laminare Grund­strömungen mit orts­unabhängigen Scher- und Wirbelstärken sowie addierten lokalen nicht­linearen Störungen durchgeführt, zunächst jedoch nur für den stationären Fall (siehe Schritt 3 für die dynamische Behandlung).
Beim Vergleich zeigt sich, dass die kinetischen Eichfeld­terme mathematisch – bis auf Rauminversion – dieselben Transformations­eigenschaften aufweisen wie die Konvektions­terme der Navier-Stokes-Gleichungen. Die Eichfelder werden demnach als Konvektions-Strömungsfelder interpretiert und entsprechend skaliert. Interessant ist, dass die Konvektions­terme in der traditionellen Herleitung aus der substantiellen Ableitung entstehen, hier jedoch als Teil des Spannungs­tensors eingeführt werden.

Weitere mögliche Links zur Herleitung: (siehe Cauchy-Eulersches Bewegungsgesetz, sowie Einsetzen des Herleitung für isotrope kompressible Newtonsche Fluide)

Legende Abb 1a:
Dies ist ein Problem für Theorien zur Turbulenz-Entstehung, wo versucht wird, den Einfluss von Störungen entlang von Strom- oder Bahnlinien aufzusummieren. Instabile Bahnlinien machen diese numerische Integration ungenau und verringern ihre Aussagekraft (kleine Integralzeichen).

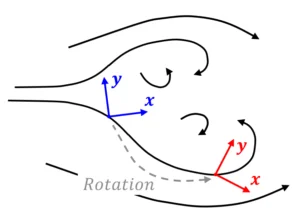
Traditioneller­weise wird in der Fl‌uid­mechanik ein Zeitbegriff eingeführt, welcher die Zeit als fort­schreitenden Parameter entlang einer Linie betrachtet (Abbildung 1a). Dieser Ansatz führt zur substantiellen Ableitung und dadurch zu den nichtlinearen Konvektions­termen in den Navier-Stokes-Gleichungen. Die Para­metrisierung entlang einer Linie ist jedoch nichtlokal und damit im allgemeinen nicht kompatibel mit Eichfeld­theorien und der darauf angewendeten Störungs­rechnung.
Da jedoch die Konvektion – wie in Schritt 2 gezeigt – in der Feldtheorie bereits durch die kinetischen Terme der Eichfelder einkalkuliert ist, reicht es, für die noch unberücksichtigte Dynamik einen lokalen Zeitbegriff einzuführen. Dies erfolgt durch Wick-Rotation, wodurch ein mit Eichfeld­theorien kompatibler, kovarianter Zeit­begriff eingeführt wird (Abbildung 1b).
Spannenderweise erlaubt es die so erhaltene Wick-rotierte Form, die in der Störungs­rechnung eingebrachten Störungen als Wellenpakete zu interpretieren, was wiederum sehr ähnlich ist zu traditionellen störungs­theoretischen Ansätzen der Fluidmechanik (siehe z.B. Lineare Stabilitätstheorie oder e^N-Methode).
Die für die Wick-Rotation vorauszusetzenden mathematischen Bedingungen (Osterwalder–Schrader Theorem) werden diskutiert, mit Fokus auf den ungewohnteren Eigenschaften wie der Reflektions-Positivität. Dieser und die folgenden Schritte werden in den bestehenden Manuskripten für zwei­dimensionale inkompressible Fluide durchgeführt.

Abbildung 1 Konvektion in der Quantenwirbeltheorie

a) Schematische Darstellung der Entwicklung eines Fluidvolumens (blaue Raute) entlang der Zeitachse. Das Fluidvolumen verändert sich sowohl unabhängig von der Umgebung (Verzerrung der Raute), als auch durch den Transport entlang der variierenden Bahnlinie, genannt Konvektion (blaue Linie). In turbulenten Strömungen können minimale Änderungen der Startbedingungen die Konvektion stark beeinflussen (alternative graue Bahnlinie). Dies ist ein Problem, wenn versucht wird, Störungen entlang der Bahnlinien aufzusummieren, wie dies bei der Modellierung von Turbulenz-Entstehung gemacht wird (kleine Integralzeichen).
b) In der Quantenfeldtheorie sind die Konvektionsterme in Form von Eichfeldern bereits im Spannungstensor an der Stelle t₁ enthalten. Sie können in diesem Sinn als eine Projektion der Konvektionsanteile auf Position t₁ verstanden werden (blau gestrichelte Pfeile).
c) Der Pfadintegralformalismus ermöglicht im Prinzip eine Umordnung der Terme, so dass zuerst über die Konvektionsterme als Störung und erst danach über die zeitliche Entwicklung des Systems integriert werden kann (blaues Band). Indem Störungen höherer Ordnung berücksichtigt werden, lässt sich ggf. der Gültigkeitsbereich erweitern (grünes Band). Der Vorteil: Für viele dieser Integrale sind analytische Lösungen bekannt.

Die Quantisierung der Theorie an und für sich ist an dieser Stelle relativ unproblematisch. Da von Beginn weg nicht Teilchen, sondern Felder betrachtet werden, ist der Schritt von Feldern zur Operatorform direkt möglich. Es müssen jedoch geeignete Rand­bedingungen und eine Normierung gefunden werden. Der realisierte Vorschlag betrachtet einzelne Fluidpartikel basierend auf kinetischen Parametern realer Fluidmoleküle (kinetischer Durchmesser, mittlere freie Weglänge) und führt periodische Rand­bedingungen ein.
Die quantisierte Theorie erlaubt die Interpretation der Felder als laminar fliessende Quasi­teilchen («Laminar­teilchen») mit Fermi-Dirac-Statistik, sowie Quasi­teilchen mit reinem Drehimpuls («Elementar­wirbel»), welche der Bose-Einstein-Statistik gehorchen.

In der Wick-rotierten und quantisierten Form kann die Theorie in Pfadintegral­form formuliert werden (Abbildung 1c). In diesem Rahmen werden die Eigenschaften der freien Felder erläutert und die Störungs­terme zweiter Ordnung werden als Feynman-Graphen angegeben (Abbildung 2). Die Störungs­rechnung wird dazu benutzt, einen Wirkungs­querschnitt für die Streuung zwischen Laminar­teilchen und Elementar­wirbeln zu berechnen, sowie die durch die Streuung verursachte Frequenz­verschiebung der Wirbel-Drehfrequenz.

Abbildung 2 Beispiel-Feynman-Diagramme

Zwei Beispiel-Feynman-Diagramme zweiter Ordnung (mit zwei Knotenpunkten), die in der Summe das invariante Matrixelement eines Pfadintegrals bilden. Diese zwei Diagramme beschreiben die Streuung eines Elementarwirbels (wellenartige Linien) an einem Laminarteilchen (gerade Linien) im zwei­dimensionalen inkompressiblen Fall.
Die Diagramme werden nach bekannten Regeln berechnet und überlagert, um schlussendlich das Pfadintegral auszuführen. Als Resultat erhält man eine Wahr­scheinlichkeits­landschaft der möglichen Endzustände des Systems.

Als erste Anwendung wird der Umschlags­punkt von laminarer zu turbulenter Strömung über einer Platte betrachtet (Übersicht in Abbildung 3, Detail­betrachtung in Abbildung 4). Diese Anordnung dient als Basismodell für Strömungen um Trag­flächen­profile und ist deshalb gut untersucht. Zudem kann der initiale Umschlag­punkt von laminarer zu wellenförmiger Bewegung (Tollmien-Schlichting-Wellen) mittels zweidimensionaler, inkompressibler Modelle abgeschätzt werden.
Das Modell betrachtet die Streuung zwischen Laminar­teilchen und Elementar­wirbeln auf Höhe der Impulsverlustdicke in der Grenzschicht über der Platte. Bei der Streuung gibt es einen Drehimpuls­übertrag, wenn die lokalen Reibungs­kräfte zwischen den laminaren Fluidschichten übertroffen werden. Über viele Streu­prozesse summiert führt dies sukzessive zu einer Angleichung der Dreh­frequenzen der Elementar­wirbel und schliesslich zu einer Resonanz­bildung im Frequenz­bereich der erwarteten Wellen­bewegung.
Qualitativ liefert das Modell einen möglichen Ansatz zur Erklärung der Entstehung von Turbulenz aus mikroskopischen Störungen. Zudem kann als Resultat der Berechnung eine analytische Formel für den initialen Umschlags­punkt angegeben werden. Dies ist neu, bisher sind dazu nur numerische Berechnungs­methoden bekannt.

Abbildung 3 Übersicht Grenzschichtströmung

Schematische Darstellung einer Grenzschichtströmung (hellblau) über einer ebenen Platte (grau). Eine Strömung mit der Geschwindigkeit v_∞ trifft von links auf eine Platte. Die Strömung verlangsamt sich oberhalb der Platte auf das laminare Geschwindigkeitsprofil v₁ (blaue Pfeile), wobei die Impulsverlustdicke δ₂ (rot) eingezeichnet ist. Stromabwärts erfolgt der Übergang zu einer turbulenten Grenzschicht, beginnend mit charakteristischen wellenartigen Strömungsmustern, den Tollmien-Schlichting (TS)-Wellen. Der Übergangsbereich wird in Abbildung 4 im Detail dargestellt.

Es gibt einige weitere Sektionen, die sich mit technischen Details und mathe­matischen Frage­stellungen befassen. Diese sollten in zukünftigen Versionen gekürzt und besser integriert werden. Falls dies nicht möglich ist, sollten sie im Anhang platziert werden.

Die detaillierte mathematische Herleitung der Quantenwirbeltheorie ist in zwei wissenschaftlichen Manuskripten formuliert, welche als pdfs zum Download bereit stehen.